ΙΠΡΕΤΕΑ
Εκπαιδευτικές Δραστηριότητες
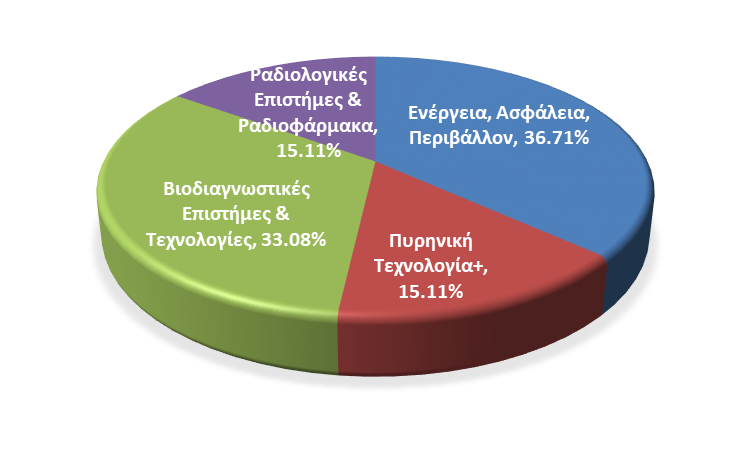
Εκπαιδευτικές δραστηριότητες ανά Ερευνητική Περιοχή
Το ΙΠΡΕΤΕΑ έχει μακρά φήμη και ισχυρή δέσμευση στη μεταπτυχιακή εκπαίδευση και κατάρτιση, από την ίδρυση του ΕΚΕΦΕ «Δημόκριτος» στη δεκαετία του 1960. Οι ερευνητικές μας ομάδες εμπλέκονται σε διάφορες εκπαιδευτικές δραστηριότητες, συμπεριλαμβανομένης της εποπτείας των μεταπτυχιακών φοιτητών, των υποψηφίων διδακτόρων και νέων μεταδιδακτορικών συνεργατών, και στους τέσσερεις διαφορετικούς ερευνητικούς τομείς του ινστιτούτου. Σε ορισμένες περιπτώσεις, οι μεταπτυχιακές ερευνητικές εργασίες μπορούν να υπάγονται σε δύο τομείς ή να γίνονται σε συνεργασία και με άλλα ινστιτούτα του «Δημόκριτου».
Αν ενδιαφέρεστε να πραγματοποιήσετε τη διατριβή σας στο ΙΠΡΕΤΕΑ, μπορείτε να βρείτε περισσότερες πληροφορίες στους παρακάτω κόμβους:
Διδασκαλία σε προπτυχιακό και μεταπτυχιακό επίπεδο
Πολλοί από τους ερευνητές μας είναι προσκεκλημένοι λέκτορες σε διαπιστευμένα μεταπτυχιακά προγράμματα που διοργανώνονται από Πανεπιστήμια στην Ελλάδα και το εξωτερικό, την Ελληνική Επιτροπή Ατομικής Ενέργειας και τον Διεθνή Οργανισμό Ατομικής Ενέργειας (ΔΟΑΕ). Εκεί παραδίδουν μαθήματα που κυμαίνονται από Ακτινοφυσική, Ασφάλεια Πυρηνικών Αντιδραστήρων, Πυρηνικές Αναλυτικές Τεχνικές, Βιομηχανική Ασφάλεια, Περιβάλλον και Ηλιακή Ενέργεια, έως Ραδιοφαρμακευτικά προϊόντα, Κλινική Χημεία, Μοριακή Διαγνωστική και Χημεία Πρωτεϊνών.
Δράσεις πληροφόρησης
Οι ερευνητικές και εκπαιδευτικές μας δραστηριότητες παρουσιάζονται σε τελειόφοιτους και απόφοιτους Πανεπιστημιακών και Πολυτεχνικών Σχολών κατά τη διάρκεια του ετήσιου Θερινού Σχολείου του ΕΚΕΦΕ «Δημόκριτος», με τη μορφή διαλέξεων, εργαστηριακών επιδείξεων και περιηγήσεων στα εργαστήρια του ΙΠΡΕΤΕΑ.
Επιπλέον, συμμετέχουμε στις τακτικές επισκέψεις που διοργανώνονται από το Γραφείο Εκπαίδευσης του ΕΚΕΦΕ «Δημόκριτος», όπου υποδεχόμαστε αρκετές εκατοντάδες μαθητές Λυκείου που επισκέπτονται τα εργαστήριά μας κάθε χρόνο. Κάνουμε επίσης διαλέξεις και επιδείξεις που απευθύνονται στο ευρύ κοινό, π.χ. κατά τη διάρκεια των ετήσιων εορτασμών στο πλαίσιο της Ευρωπαϊκής Βραδιάς Ερευνητή.
Βίντεο παρουσίασης των εκπαιδευτικών δραστηριοτήτων του ΙΠΡΕΤΕΑ:
Υπεύθυνοι Εκπαίδευσης ΙΠΡΕΤΕΑ

Δρ. Νίκος Παπαδημητρίου
(Ενέργεια, Ασφάλεια και Περιβαλλοντικές Τεχνολογίες, Εργαστήριο Ηλιακών & άλλων Ενεργειακών Συστημάτων)



